Geometric Sphere
Implementation
The implementation of the geometric sphere intersection is very straightforward. The only thing we need to take care is that the ray direction vector is normalized in the derivation, which is not in pbrt. The square of radius is pre-calculated in the constructor to speed up the intersection determination.
Trick - Carmack's fast square root
Square root is a costly operation in geometric sphere intersection (for normalization of ray direction vector). I use the fast square root method developed by John Carmack [Carmack]. It uses the special characteristic of IEEE floating point format. The original code can be found in Quake III open source codes (code/common/cm_trace.c):
float fsqrtf( float number ) {
long i ;
float x , y ;
const float f = 1.5F ;
x = number * 0.5F ;
y = number ;
i = * ( long * ) & y ;
i = 0x5f3759df - ( i >> 1 );
y = * ( w * ) & i ;
y = y * ( f - ( x * y * y ) );
y = y * ( f - ( x * y * y ) );
return number * y ;
}
Theoretically, fsqrtf is 4 times faster than sqrtf since there is no recursive. However, the overall speed-up is small.
Result
The simulation results show that the speeds of geometric intersection and algebraic intersection are almost the same.
Octree-R
A modified octree based on octree-R [Whang95] is implemented. I tried two different intersection methods, which are both faster than the previous one in [Gargantini93]. Also both methods do not face the precision problem in [Gargantini93]. In this work, I have many discussions with Chihyuan Chung. There may be some overlapping routines in our codes, but we develop them independently.
Build Tree
In [Whang95] they propose to find a method to find the splitting plane for each axis independently. For an intermediate node, the splitting plane is chosen between object median and spatial median. We modify this method slightly so we can re-use the kdtree code in pbrt. First the splitting plane can be any plane of the BBox's of objects which belong to this node. Second, the splitting cost is the same as the one used in pbrt, and we apply it to all three axes.
Some parameters are modified to improve the performance. maxDepth is halved, and one-third in some scene due to the memory capacity. More badRefines are acceptable before forcing the node to be a leaf node.
Intersection Method One
For each node, we need to determine the intersections of the ray and its 8 child nodes. In original BBox intersect(), we check the intersection of the ray and 3 slabs. However, for 8 child nodes, there are only 6 planes of BBox and 3 splitting planes. Therefore, the 3 slabs of each child node must be chosen from these 9 planes, which can be tabulated. Specifically, we calculate 9 intersections of the ray and 9 planes for each node, and use them to determine which child nodes are hit. In this way the number of intersection checking is decreased from 48 to 9.
We also sort child nodes according to the distance of the hit point to the ray origin. Like the rule in kdtree, the closer child nodes are checked before the farther ones.
Intersection Method Two
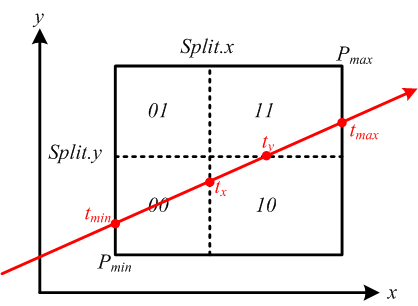
Inspired by the method proposed in [Gargantini93], we find a new method to find the intersections of child nodes. We can also determine the intersection order simultaneously. Here we give a 2D example, as shown in the figure below.
In the intersection determination function, for a node, we need to find its child nodes to be checked, and they should be checked from near to far. First we can find the intersections of the ray and the bounding box, and the intersections of the ray and the splitting planes. In this example they are denoted tmin, tmax, tx, and ty, and the order of them can be determined easily. We only need to sort tx and ty if they are within (tmin, tmax).
In [Gargantini93], the child nodes are chosen according to the end points of each line segment. Comparing the intersection points and the split planes, we can calculate bitx and bity, and the index of the child is 2*bitx+bity. For example let px = ray.o + tx*ray.d and py = ray.o + ty*ray.d, we can calculate:
px.x = Split.x, py.x > Split.x -> bitx = 1,
px.y < Split.y -> bity = 0,
index = 2*1+0 = 2.
So the child index is 2. However this operation may be erroneous because although px.x equals Split.x theoretically, it can be false due to the limited precision.
We find a new method to determine the indices of child nodes. First, pmin = ray.o + tmin*ray.d seldom falls on the splitting planes, so we can use it to find the first child node directly. Second, we notice that the index of the next child node and the index of the current child node will only be different in the bit of the shared splitting plane. In this example, we know the ray leave the child 0 at px, which is the intersection of Split.x. Therefore, the index of the second child is XOR(00,10) = 10. Applying this rule again on the second node, the index of the third node is XOR(10,01) = 11. In 3D application, we need to apply this rule at most 3 times for each node, since there are at most 4 child nodes to be intersected. Note that in this method we do not need to compare the location of intersection point with the intersected plane.
I further optimize this routine in many ways. First the above XOR operations can be tabulated first, since there are only 8x3 = 24 cases. Second, using this method we do not need to save the bounding box of each node anymore. Third, we need to calculate pmin in each recursion, but it may be calculated many times (pmin of the current node is still the pmin of the first child node). Therefore I save pmin in the todoList.
Result
The main problem of octree is that a object will be in more than one leaf nodes, and the repeating rate is much higher than that of the kdtree. For the intersection method one, the speed ratio ranges from 2.17 to 2.53 when maxDepth is half of the kdtree. For the scene plant-directsun, maxDepth is one-third and the ratio is 3.24. For intersection method two, the speed ratio ranges from 1.48 to 1.59 for the first 4 scenes and 2.03 for plant-directsun. On average method two is much better.
Downloads
Sphere:
I use two #define, USE_SHPERE_GEO and USE_FAST_SQRT. You can set them as 0/1 arbitrarily to switch the mode.
Source code: sphere.cpp (Put this in src\shapes)
Octree-R
I use two #define, USE_METHOD_ONE and USE_METHOD_TWO to switch between two intersection methods.
Source code: octreer.cpp (Put this in src\accelerators)
MS .NET Project file: octreer.vcproj (Put this in src\win32\Projects)
Experimental results:
References
- I. Gargantini and H. Atkinson, Ray Tracing an Octree: Numerical Evaluation of the First Intersection, Computer Graphics Forum 1993.
- K.-Y. Whang et. al., Octree-R: An Adaptive Octree for Efficient Ray Tracing, IEEE TVCG 1995.
- John Carmack's Magical Square Root Implementation In Quake III (link)